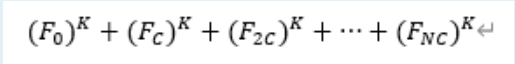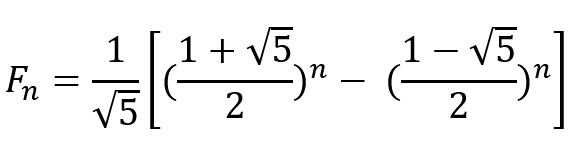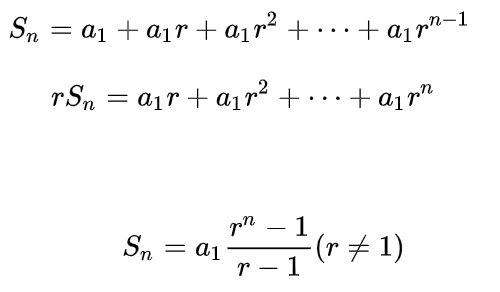传送门

题意是说给两个字符串|n|\leq10^5,|m|\leq20。
有|q|\leq10^5次询问，每次给出n的一个区间[l,r]。

求区间内与字符串M的编辑距离（只有插入和删除操作）。

---

做法是先发现插入操作是无用的，因为再某个点插入可以等价转化为把对面字符串的对应位置删掉。所以ans=[l,r]+|m|-2LCS

那如何快速求最长公共子序列，要先发现m其实很小只有20。所以可以用另外一种求LCS的方法：

f[i][j]表示B[i]为止的，长度为j的LCS的A串的最短前缀长度。

同时用另外一个g[i][j]表示A[i] \to A[n]内字符j第一次出现的位置。

f[i][j]=min(f[i-1][j],g[l+f[i-1][j-1]][b[i]]-l+1)

这样求一次LCS复杂度为O(m^2)

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int e[maxn][30], f[22][22];
char s[maxn], p[30];
int main()
{
    freopen("1012.in", "r", stdin);
    freopen("r.txt", "w", stdout);
    cin.tie(0); cout.tie(0); ios::sync_with_stdio(0);
    int T; cin >> T;
    while(T--)
    {  
        cin >> (s + 1) >> (p + 1);
        

… Read the rest

传送门

题意是说给 N, C, K 求这样一个东西：

其中F_{NC}表示斐波那契数列的第NC项。

---

做法是先查一下斐波那契数列的通项公式：

找到其中根号5的二次剩余。

383008016^2 ≡616991993^2≡5 (mod 10^9+9)

然后就可以替换掉通项里的东西。

F_n=C(A^n-B^n)

可得

F_{cn}^k=C^k(A^{cn}-B^{cn})^k

\sum\limits_{i=0}^n F_{ci}^k=C^k\sum\limits_{i=0}^n(A^{ci}-B^{ci})^k

对其二项式展开, 并变换枚举顺序

\sum\limits_{i=0}^nF_{ci}^k= C^k\sum\limits_{i=0}^n \sum\limits_{r=0}^k \binom{k}{r}(A^{ci(k-r)}B^{cir}(-1)^r)

\sum\limits_{i=0}^nF_{ci}^k= C^k \sum\limits_{r=0}^k \binom{k}{r} (-1)^r \sum\limits_{i=0}^n (A^{ci(k-r)}B^{cir})

然后观察到内层的 \sum\limits_{i=0}^n (A^{ci(k-r)}B^{cir}) 其实是以(A^{c(k-r)}B^{cr})为公比的等比数列（几何级数），可以直接使用公式求和。

• 注意本题从0累加到n实际上有n + 1项，求几何级数的时候需要注意。但是第0项等于0，所以也可以看作从1开始枚举，用通项的时候单独减去1。两种处理方法都可以。

• 第二个需要注意的点是公式仅适用于r =\not 1。如果r=1直接用r * n或者r*(n+1)即可。取决于上面一步是什么处理方法。

在实际代码中，每一轮的公比实际是上一轮的A和B自乘一个单位，所以可以先预处理。不然这题时间卡的非常紧会T掉。

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod = 

… Read the rest

转送门

题意是说给n个点m条边，能否选出一些边使得每个点恰好又d[i]个度。d[i]只有1或者2。

做法是每条边拆成x, y两个点，互连。边的两个点i拆成d[i]个点与x连，j拆成d[j]个点与y连。

然后做一般图匹配，判断是否有完美匹配。

可以被证明，当x取模S域的随机数时，错误概率不会高于n/S

于是建起这个矩阵高斯消元即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
mt19937 mrand(random_device{}()); // mrand是给定随机数种子的的大随机数对象
int rnd(int x) { return mrand() % x;}
const double eps = 1e-6;
const int maxn = 433;
ll a[maxn][maxn];
ll mod = 1e9 + 7;
ll ksm(ll n, ll k)
{
    ll res = 1;
    while(k)
    {
        if(k & 1) res = res * n % mod;
        n = n * n % mod;
        k >>= 1;
    }
    return res;

… Read the rest

传送门

---

题意是给n个数，问从中选1个、2个、3个….数，最大的异或和是多少。选数可以重复。

---

用一个数组，把出现的数字在数组对应下标处 + 1 .

然后做一次下标为异或运算的卷积。C_i=\sum\limits_{i=j \oplus k}A_j* B_k 

卷一次代表选两个数，卷 n 次就代表选 n 个数。卷积结果C_i若不为零，则i表示可以被异或出来。

因为数字最大只有18位，所以理论上来说18次之后最大数就会出现（每个数至少贡献一位）。但是以防万一可以多整几次。之后最大数就和选 n – 2 个数字是一样了。

优化下标为位二元运算的卷积有一个算法叫：快速沃尔什变换（FWT）。

思想是将原序列 A 构造成一个新的序列 FWT[A] 使得卷积可以变成对应项相乘，把复杂度优化到线性。

关于几种运算的构造方法，记一下结论就可以了。结论在此

#include<bits/stdc++.h>
using namespace std;
const int maxn = (1 << 18) + 233;
typedef long long ll;
const ll mod = 1e9 + 7;
ll inv = 0;
ll ksm(ll n, ll k)
{
    ll res = 1;
    while(k)
    {
        if(k & 1) res = res * 

… Read the rest

原题传送门

中文题面

---

题意是有Q个区间询问，每次询问只能得到区间内未被覆盖的位置。
要求一种顺序，使得这Q个询问里的最小值最大。

必须首先发现：最后一个人所得到的座位数量，和前面Q-1个询问的顺序是没有关系的。
所以可以得到一个贪心策略：
1. 从最后一个人开始，枚举谁能得到最多的座位。假设是第X个询问。
2. 去掉第X个询问，再重复步骤一。
3. 重复以上步骤直到询问为空。从得到的答案里取一个最小值即是答案。

如果每一步都暴力枚举，离散化以后复杂度是O(Q^2)的(排序以后扫描)。
可以建立一颗长度为N的线段树，线段树上每个点存储当前区间被哪些询问完全覆盖，和区间内点的最少覆盖次数。
考虑到执行覆盖和撤销覆盖的操作都是成对出现的，当前线段被哪些区间完全覆盖可以不用下传懒标记，参考 亚特兰蒂斯 的做法。在往下走的时候，仅仅对第一次遇见的区间进行标记，撤销的时候也无需往下走。
以样例来解释，仅需要在这些有颜色的区间上记录有哪些线段对其进行了覆盖即可。

区间最小值就用普通的懒标记，优化到每次修改是NlogN。
对于每次找答案，在线段树中往下走找到那些数值为1的点，同时把值赋成无穷大，以后不再访问这个点，在往上回溯的时候在那些只有一个线段覆盖的区间加上这些1的个数。
然后取得值最多的那个线段执行撤销操作。找到最多的区间这一步可以再用一颗线段树维护。
因为记录区间不需要任何顺序，所以用Hash表即可，STL里的unordered_set就能满足。
总的复杂度就成了Nlog(N+Q)

#include<cstdio>
#include<algorithm>
#include<unordered_set>
#include<iostream>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int maxn = 1e6 + 23;
const int INF = 0x3f3f3f3f;
int n, q;
PII seg[30300];
struct NodeQ {
    int l, r;
    int v;
}trQ[30300 * 4];
void buildQ(int u, int l, int r)
{
    if (l == r) 

… Read the rest

传送门

---

给定N个数，代表N个景点的权值，必须顺序参观完。每天最多参观K个景点，但是必须严格N/K+(N%K!=0)天参观完。当天的收获为当天景点的最大权值，问总收获最大是多少。
N和K都小于1E6

---

先考虑这样一种状态表示：
如果把每K个景点分成一份，最后一份可能会少K-N%K个。记为M。
假设每天的目标是一份。
f[i][j] 表示前 i 天偷了 j 天懒。也就是说本来应该走i * k 个景点，但是只走了i * k – j个。
很明显只要确定了偷懒天数，第x天停留的位置就固定了。所以第二维也可以换为停留的位置。
假设停留在下图的i点。
很明显f[x][i]=\max\limits_{j=i-k \to st} (f[x-1][j]+\max\limits_{k=j\to i}a[k])

---

由于每个阶段都是固定长度，所以很好判断当i%k==0的时候肯定是一个阶段的结束。
这样可以把dp状态优化到一维。

然后由于dp[j]+maxA[j+1,st]这一部分是不变的，可以在每个阶段结束的时候预处理出来。
用树状数组维护这个值的后缀区间最大。同时mxdp[x]记录dp[x,st]最大值和mxA[x]记录A[x+1,st]的最大值。下一个阶段可以直接使用。

当下一个阶段开始的时候，让a[i]和mxA[j]进行比较，如果a[i]更大，那么更新[j,i]的树状数组。同时j往后退。

当i向前移动一步的时候，同样也是更新[j,i]的树状数组。

次数树状数组[j,i]的最大值就是dp[i]的值。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 233;
ll c[maxn], 

… Read the rest

这是个链接 -Z函数作用同扩展KMP

有字符串s，z[i]表示s[i]开始的字符串与s[0]开始的字符串的最长公共前缀

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 233;
char str[maxn];
int ne[maxn], z[maxn];
int main()
{
    int T; scanf("%d", &T);
    while(T--)
    {
        scanf("%s", str + 1);
        int len = strlen(str + 1);
        for(int i = 1; i <= len; i++) z[i] = 0;
        z[1] = len;
        for(int i = 2, l = 0, r = 0; i <= len; i++)
        {
            if(i <= r) z[i] = min(z[i - l + 1], r - 

… Read the rest

股票问题汇总

股票问题，指给定一系列数列，可以在某些天以当天价格买入，也可以在某些天以当天价格卖出。

按照买卖规则，可以分为：
1. 不能进行多笔交易；买股票之前只能先把手上的股票卖出。一般此类题是dp。
2. 可以进行多笔交易；手里可以同时持有多只股票。一般要贪心。

股票问题的核心是发现如何使得手里的资产最多。

无论是哪种模型，都可以看成如果第二天价格更高就卖，大不了可以反悔（可以以这天的价格再把卖掉的股票再买回来）。

问题1

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 233;
int w[maxn], f[maxn][110][2];
int main()
{
    int n, k; scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++) scanf("%d", &w[i]);
    memset(f, 0xcf, sizeof f);
    for(int i = 0; i <= n; i++) f[i][0][0] = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= k; j++)
        {
            f[i][j][0] = max(f[i - 

… Read the rest