千题目标CategorySubscribe

传送门

题意是说给一颗树的拓扑序列，再给它的dfs序列。两次根可能不同。

问你能不能构造出原树。

首先要分析两种序列的性质。

拓扑序和dfs序，排在后面的点肯定是前面的点的子孙。所以后面的点与前面的点连边不能超过1条。

那么有个很简单的想法：

使得两个序列都满足每个点与前面出现的点最多有一条边。

然而很遗憾这是不对的。下面给出一个反例

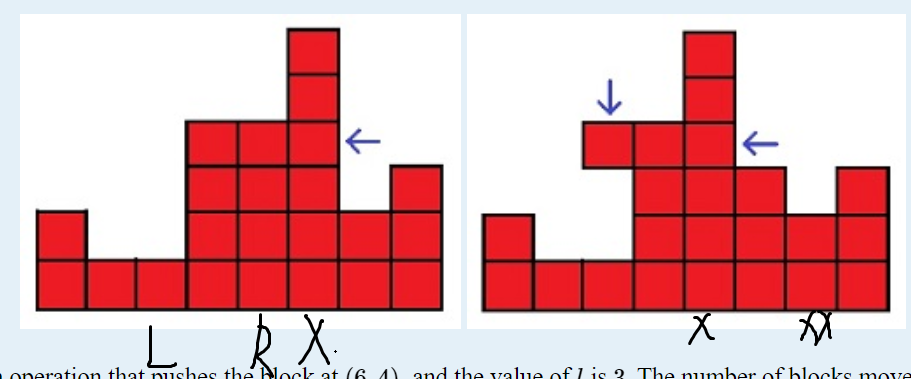
top：6 4 2 1 3 5

dfs：1 2 3 4 5 6

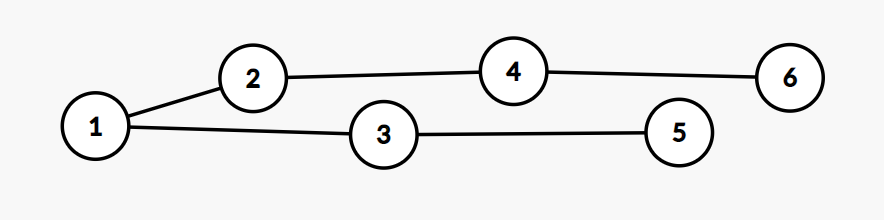
很显然这样一种构造只能满足拓扑序，不能满足dfs序。

要满足dfs序，还需要满足要满足一个条件：一个点要么是叶子（与后面不连边），要么是某个子树的根（必须与紧接着后面的一个点连边）。

所以需要构造一棵合法的树，每个序列的节点要满足两个两个条件：1. 每个点最多与前面一个点相连。 2. dfs序中的每个点还要满足要么后面挨着的一个点与他相连，要么后面没有点和他相连。

具体做的时候，两个指针i, j枚举dfs序，每次由B[j]向B[i]连边，保证 i < j 而且 i 在过程中单调不减，即可让dfs序列满足条件。同时让B[i]在A中的位置单调不增，即可让拓扑序满足第一个条件。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
mt19937 mrand(random_device{}());
int rnd(int x) { return mrand() % x;}
const int N = 2e5 + 233;
int a[N], b[N], pos[N];
int main()
{
    // time_t startt = clock();

    // cin.tie(0); cout.tie(0); ios::sync_with_stdio(0);
    int n; 

… Read the rest

传送门

题意是说有一些方块堆积起来的积木。有两种操作。

1 x y 是把第x行从下数第y个方块往左推一个。这会导致有一些方块悬空，这些悬空的方块会受到重力的影响下落。如果可以移动输出移动的方块数量。

2 x 是输出第x列的方块数量。

根据样例分析。

1. X往左走一格，可以看作X和X+1之间插入了一个(y-1)的数。
2. L是X左边第一个小于y的数，假设L的是第rank个，那么R就是第rank+2个。L和R之间那个数删掉即可。
3. L会加上前面那个柱子里掉下来的一些方块。

具体来说，先找到排名x的点X，排名x+1的点XX，把X Splay到根，再把XX Splay到X下面，在XX的左儿子插入一个(y-1)。

找到X以前的第一个小于y的点，根据size求出它的排名rank，顺便求出排名rank+1的D，R的排名rank+2，求出点R，把L Splay到根，R Splay到L下面，删掉… Read the rest

小强向你请教了一个奇妙的数学题:给定两个数n和m,小强可以通过对n里面的数位进行重新排列。

现在小强请你帮他计算出经过重新排列后所得到的数中满足不含有前导零并且能够整除m的数字有
多少个?

注意:相同的数只算一次

n < 1e15
m < 100

这题是SCOI2007魔改了条件

原题的方案里可以包含前导零。其实只需要判断一下如果当前状态是全0则表示有前导零的状态，不进行转移即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
mt19937 mrand(random_device{}());
int rnd(int x) { return mrand() % x;}
const int N = 16, M = 110;
ll n, m;
ll f[1 << N][M];
vector<int> v;
bool vis[10];
int ze = 0;

int main()
{
    // time_t startt = clock();

    cin.tie(0); cout.tie(0); ios::sync_with_stdio(0);
    int T; 
    T = 1;
    while(T--)  
    {
        cin >> n >> 

… Read the rest

传送门

题意说给n个高度为ai的板子，你可以用宽度为1的刷子横着涂色或者竖着涂色，当遇到空隙或者边缘的时候停止，不可以拐弯。问最少多少次能涂完。

做法是贪心，对于一个区间，如果我要横着涂，那些能一笔涂完的地方我一定要一笔涂完。

而对于一个矩形，很容易算出来到底横着还是竖着划算。

于是对于每个区间，我先把能横着涂的涂完（一个矩形），然后递归没涂的两个部分。

#include<bits/stdc++.h>
using namespace std;
const int N = 5e3 + 233;
int a[N];
int solve(int l, int r, int u)
{
    if(l > r) return 0;
    int h = a[l], idx = l;
    for(int i = l; i <= r; i++) h = a[i] < h ? a[idx = i] : h;
    return min(r - l + 1, solve(l, idx - 1, h) + h - u + solve(idx + 1, r, h));
}
int 

… Read the rest

传送门

题意是说给一个网格，每个格子有一个权值，选择其中一些格子涂黑，要求黑色直接不能临边。然后还需要找到一条哈密顿回路。

问如何选择黑色的格子使得权值最大。

插头DP，0表示无插头，1、2表示对应联通分量的插头，3表示黑色格子的插头。

#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
mt19937 mrand(random_device{}());
int rnd(int x) { return mrand() % x;}
const int N = 100007;
int n;
int a[16][16], state[2][N], dp[2][N], now;
int G(int k, int x) {return (k >> (x << 1)) & 3;} // 轮廓线k的第x位状态
int F(int k, int x) {return k << (x << 1);} // 编码第x位的状态k
// unordered_map<int, int> st;
int fst[N], pre[N], mk[N], mt, tot;
void init()

… Read the rest

题目源于字节跳动2021秋招研发第二场第二题。

题意是说，给长度为n<10^5的字符串，里面包含十六进制数字（0~F），要求让这个字符串不能包含‘0010’这个子串，问最少要删除多少次。

其实这个子串很特殊，对于任意一个字符串，我总能找到一种方法使得我删除一个字符之后0010的个数减少一个。那么就是求一下出现了多少次0010即可。

但是如果给你的串不是0010而是一个随机的串呢？

又到了经典的“不包含子串”时间了。这种题一般是在KMP上dp。

先对模式串做一次KMP。

枚举原串的每一位，再枚举KMP的每个状态，若做匹配的时候没有匹配到结尾，说明不含模式串，此时可以直接对状态取最小，如果匹配到最后了则不能进行转移，因为此时表示含子串。

在原串i匹配到模式串j的情况下，如果我删除这一位，那么原串i+1则匹配模式串j，同时删除次数加一。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
mt19937 mrand(random_device{}());
int rnd(int x) { return mrand() % x;}
int ne[10], f[100005][10];
char str[100005];
char p[10] = " 0010";
int T;
int main()
{
    // time_t startt = clock();
    int m = 4;
    for(int i = 2, j = 0; i <= m; i++)
    {
        while(j && p[i] != p[j 

… Read the rest

传送门

题意是说，在一个无限长的坐标轴上，给n个报点。表示在t_i时间，在x_i这个位置出现了一个人。每个人会一直往左跑或一直往右跑。起点终点均未知。

问根据给你的信息推测，最少有多少人同时在跑步。

---

做法是，若出现则把平面坐标上(t_i,x_i)的点染黑。由于每个人只能朝一个方向跑，那么每个点会产生一条斜率为1和斜率为-1的直线。

问题转化为选择最少的直线覆盖这n个点。

具体写的时候，把坐标绕原点旋转45度，则所有直线平行于 x轴或 y 轴，每个点(x,y)从x向y连一条边。若选择x那么表示选择了平行于x的直线，若选择y则表示选择了平行与y的直线。

问题继续转化为，对于每条边，至少要有一个点被选择。即最小点覆盖问题。也就是二分图的最大匹配。

边数比较多，大概是四倍于点，点最多是10^5，所以做的时候用网络流dinic来匹配，可以到O(n\sqrt n).

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
mt19937 mrand(random_device{}());
int rnd(int x) { return mrand() % x;}
const int N = 1e5 + 233;
unordered_map<int, int> ux, uy;
int nx[N], 

… Read the rest

传送门

题意是说给了n个数字a，m个数字b，k个数字s。

定义了一个集合S，它表示 s 的异或运算封闭群，就是说若干个s异或起来造出来的所有数都在这个集合S里。

定义了一个匹配，取与b数组长度相同的连续一段a数组，当且仅当对应位置异或起来的数字都在S里的时候，称为匹配成功。

问有多少个段能匹配成功。

---

首先可以用一个线性基来表示这k个s所表示的线性空间。

1. 若a_i 与 b_i均能用这个线性基表示出来，那么异或出来的数一定在群里。

2. 若a_i 与 b_i只有一个不能被线性基表示出来，那么异或出来的数肯定不在群里。

3. 若两个数都不能被线性基表示出来，异或结果是可能在群里的。当且仅当把能用S表示出来的部分删掉后a’=b’。这个其实蛮明显的，比赛的时候没想到。

然后就变成了B串为模式串，A串为原串，做KMP匹配。

温馨提示：本题卡cin，不知道是不是因为HDU编译器版本太旧，关同步也没用。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
mt19937 mrand(random_device{}());
int rnd(int x) { return mrand() % x;}
int n, m, k;
const int mod = 1e9 + 7;
const 

… Read the rest

传送门

题意说给一棵树，若在任意两点之间加边，权值为路径的异或和。

在保证图联通的情况下可以删边。

求如何操作使得最后这张图的边权和最小。

做法是先发现任意两点的边权其实可以看做给定，就是到根节点的异或和。

那么先预处理出来所有点的异或和当作点权，问题转化为：给定一些点，任意两点之间连边为其二的异或和，求最小生成树。

用到了Boruvka的思想，合并两个连接边权最小的连通块。

把所有点插入trie树上，考虑任意一层的任意一个点，最优的合并必然是要合并左右子树，因为更高位是相同的，异或得 0 。而合并所需要得代价就是其左子树所有点和右子树所有点的异或最小值。

分治来求每个节点的代价，左边的值都插入trie，枚举右边查询最小值。查完以后把trie清空。直接把所有idx的点标记为0即可。

#include<bits/stdc++.h>
using namespace std;
using namespace std;

const int N = 100010, M = 3000000;

int a[N], son[M][2], idx;

void insert(int x)
{
    int p = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int &s = son[p][(x >> i) & 1];
        if (!s) s = ++ idx;
        p = s;
    }
}

int search(int x)
{
    int p = 0, res = 0;
    

… Read the rest

传送门

题意是说给两个字符串|n|\leq10^5,|m|\leq20。
有|q|\leq10^5次询问，每次给出n的一个区间[l,r]。

求区间内与字符串M的编辑距离（只有插入和删除操作）。

---

做法是先发现插入操作是无用的，因为再某个点插入可以等价转化为把对面字符串的对应位置删掉。所以ans=[l,r]+|m|-2LCS

那如何快速求最长公共子序列，要先发现m其实很小只有20。所以可以用另外一种求LCS的方法：

f[i][j]表示B[i]为止的，长度为j的LCS的A串的最短前缀长度。

同时用另外一个g[i][j]表示A[i] \to A[n]内字符j第一次出现的位置。

f[i][j]=min(f[i-1][j],g[l+f[i-1][j-1]][b[i]]-l+1)

这样求一次LCS复杂度为O(m^2)

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int e[maxn][30], f[22][22];
char s[maxn], p[30];
int main()
{
    freopen("1012.in", "r", stdin);
    freopen("r.txt", "w", stdout);
    cin.tie(0); cout.tie(0); ios::sync_with_stdio(0);
    int T; cin >> T;
    while(T--)
    {  
        cin >> (s + 1) >> (p + 1);
        

… Read the rest