G@rage

传送门

题意是每个节点有一个属性，取子树的最大或最小值。只有叶子节点有初始值，可以分别是1 – n(叶子节点个数)里面的任意一个值。问根节点最大值是多少。

很巧妙的思路。

对于每一个节点，在他及其子树中，相对大小都是确定了的。

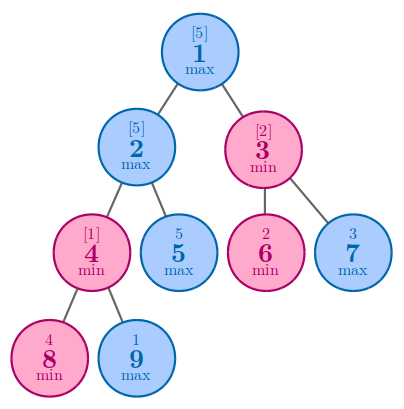
比如在上图里。
节点{4}取最小，在{8, 9}里是第二大。
节点{2}取最大，在{8, 9, 5}里是第一大。
设f[i]表示i个节点的相对大小（第几大）。
对于每个节点，都需要尽量的大。所以f[i]需要尽量小。对于取\min的点，一定是子树的rank之和。而去\max的点，一定是子树的rank1.

最后拿总数减去根节点的rank就是根节点的取值

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e5 + 233;
vector<int> G[maxn];
int c[maxn], f[maxn], cnt;
void dfs(int x)
{
    if(c[x]) f[x] = 1e9;
    for(int i = 0; i < G[x].size(); i++)
    {
        int y = G[x][i];
        dfs(y);
        if(c[x]) f[x] = min(f[x], f[y]);
        else f[x] += f[y];
    }
    if(!G[x].size()) f[x] = 1, cnt++;
}
int main()
{
    int n ; 

传送门

题意让求一个排列，字典序最大而且使得逆序对数量为k，再对这个序列按照每位乘上(n + 1) ^ i求和

第一点 : 字典序最大的排列方式肯定为9876 3 12 45这样的有四段，第一段是贪心地拿字典序最大的变成最多的逆序对，如9876 12345这样有 (5 + 8) * 4 / 2 = 26 个逆序对，如果需要28个逆序对，肯定是把 3 放在尽量前面 9876 3 12 45 ，这样就组成了四段，第一段9降序，第二段是3，第三段1升序，第四段从3 + 1升序。

接下来就变成了序列求和的问题。观察到\sum{p[i] * (n + 1)^{i}}实际上是一个公差为 1 或者 -1 的等差数列和公比为（n + 1）的等差数列相乘的来。

引理：对于首项为a_1，公差为d_1，的等差数列a_n，首项b_1，公比q的等比数列b_n。
一定存在S_n = \sum{a_i b_i} = x_1b_1 – x_{n + 1}b_{n + 1}
其中 x 为等差数列 x_1 = \frac{a_1}{1 – q}+\frac{qd}{(1-q)^2} \quad … Read the rest

又来重温一下这个经典的带权并查集题目。

本题的关系有三层 -a -b -c -，但不同的是本题的关系是有向的，也就是说a和b如果是敌对关系，那么b和a就不是敌对关系。所以反向推算关系不是简单的相加。

关系传递的本质实际上是向量的运算。

还是设 d[x] 表示 x 与 fa[x] 的关系，0 代表是同类，1 代表是x吃fa[x], 根据关系图自然2就代表x被fa[x]吃。

下面假设a的祖先是x，b的祖先是y，为简化书写，设他们的向量关系为

\vec{a} = (a,x) \quad \vec{b} = (b,y)
给出的关系设为rel = \vec{ab}

以下的向量关系均用以上符号代替，实际运算时自行带入二元组运算即可

1. 若x = y
   想要知道 \vec{ab} ，则需要 \vec{a} – \vec{b} 然后对3取模并移动到正整数
   此时得到的关系0代表ab是同类，1代表a吃b，2代表a被b吃。直接与rel进行比较即可。

2. 如果x和y不等，那么这个给出的关系肯定是合法的
   合并的时候同样fa[x] = y，\vec{x} = \vec{b} + \vec{ab} – \vec{a}

然后就可以愉快的搞了

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e4 + 233;
int fa[maxn], d[maxn];
int ff(int x)
{
    if(fa[x] == 

传送门

二分答案很好想，关键在于如何检查是否存在一个半径为r的“曼哈顿圆”能覆盖所有的空白点。

这里需要用到曼哈顿距离的另一个公式”dis(P_1,P_2) = \max{(|(x_1 + y_1) – (x_2 + y_2)|,|(x_1 – y_1) – (x_2 – y_2)|)}”

有了这个公式，发现只需要检查x+y的最大和最小，x-y的最大和最小，所对应的点是否满足即可。因为这四个点满足了其余点肯定是满足的

#include<bits/stdc++.h>
using namespace std;
const int maxn = 255;
typedef pair<int,int> pii;
vector<pii> e;
int n,m;
int mp[maxn][maxn];
bool vis[maxn][maxn];
int dir[4][2] = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
void bfs(int k)
{
    memset(vis, 0, sizeof vis);
    queue<pair<int,pii> > q; 
    for(auto i : e) q.push({0, i}), vis[i.first][i.second] = 1;
    while(q.size())
    {
        pii s = q.front().second;
        int t = 

传送门

a进制的数s，转换成b进制的数。
每次s对b取余的结果就是b进制数的低位。然后s再除以b，再重复取余，直到商0。
涉及高精度取余的操作，从高位到地位，每次s[i]%b = r，得到的余数借位到下一位的时候，由于可能不是十进制，所以下一位是r * a + s[i+1];最后所有位除法操作结束剩下的r就是一位结果

#include<bits/stdc++.h>
using namespace std;
int e[505],d[505];
string ts(string a, int x, int y)
{
    vector<int> scr;
    for(int i = 0; i < a.size(); i++) scr.push_back(e[a[i]]);
    reverse(scr.begin(), scr.end());
    vector<int> res;
    while(scr.size())
    {
        int r = 0;
        for(int i = scr.size() - 1; i >= 0; i--)
        {
            scr[i] += r * x;
            r = scr[i] % y;
            scr[i] /= y;
        }
        res.push_back(r);
        while(scr.size() > 0 && *scr.rbegin() == 0) scr.pop_back();
    }
    

传送门

一般扫描线

今天才发现我这种写法，需要把差分负值作为第二排序依据，因为差分结束的地方可能和另外一个差分开始的地方重合， 如果不清除以前的影响会造成答案变大

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int maxn = 1e5 + 233;
#define ls(x) (x << 1)
#define rs(x) ((x << 1) + 1)
struct Node{
    int l, r, dat, mk;
    #define l(x) t[x].l
    #define r(x) t[x].r
    #define dat(x) t[x].dat
    #define mk(x) t[x].mk
}t[maxn * 4];
void build(int p, int l, int r)
{
    l(p) = l; r(p) = r;
    if(l == r)
    {
        dat(p) = 0; mk(p) = 0;
        return ;
    }
    int 

传送门

最开始没想到这个模型。还贪心写了半天，发现是错的，贪不动。

这题关键在于模型的转化。转化后的题意就是求一个最长的区间，使得区间总和乘上区间最小数最小。

那其实和单调栈经典题目求最大矩形是差不多的，稍微有点不同的是本题可以看成矩形的宽度不是1，而是题目给定的数字……..

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 233;
typedef long long ll;
int n;
ll a[maxn], b[maxn], w[maxn], s[maxn];
int main()
{
    while(cin >> n)
    {
        for(int i = 1; i <= n; i++)
        {
            scanf("%lld",&a[i]);
        }
        a[n + 1] = 0;
        memset(s, 0, sizeof s);
        int p = 0;
        ll ans = 0, l = 1, r = 1;
        for(int i = 1; i <= n + 1; i++)
        {
            if(a[i] > 

传送门

题意是找一个最长的区间，使得区间内最大值-最小值 max – min 属于[m,k]

最开始想的二分长度，但实际上并不具有单调性。。
比{1, 0, 1, 3} m = 3 这组数据，当长度为2的时候所有区间都不满足，但长度为3的时候就有一个区间满足了。也就是说不存在短的区间满足，并不代表不存在更长的区间不满足。

导致没有单调性的原因就是题目要求需要满足两个条件，就破坏了单调性，如果题目只有一个限制条件k，那么就是满足单调性的，不存在更短的区间不满足k那么也不存在更长的区间满足k，因为包含段区间的长区间最大值不可能更小，最小值也不可能更大。

因为包含不满足k的区间一定需要更小，而包含不满足m的区间可能变得更大，所以用队列来做。顺序读取数据，让读到一个连续区间不满足k，就从前面缩短区间，直到满足k，当满足m的时候用长度更新答案。

可以用ST表也可以用set。

//1 0 1 3 m = 3 小区间不满足，大区间不一定不满足，不可二分
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 233;
int n, m, k;
int a[maxn];
int main()
{
    while(cin >> n >> m >> k)
    {
        multiset<int> st;
        int l = 1, ans = 0;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d",&a[i]);
            st.insert(a[i]);
            while(*st.rbegin() - *st.begin() > 

传送门

题意是每个苍蝇有两个属性，a和b，前面的苍蝇要分别和后面的苍蝇决斗，每次的分数为max(ai-aj,bi-bj)-min(ai-aj,bi-bj) (i < j) 。

可以想到

• res = ai – aj – bi + bj (ai – aj bi – bj)
• -= (ai – bi) – (aj – bj) (ai – bi aj – bj)
• 同理，当大小关系相反的时候，是Hj – Hi

所以可以先把 ai – bi 处理出来。

由于是前面的要和所有后面的决斗，所以把数据离线，从后面开始算，每加入一个点，找已经加入的点中，比他大的，比它小的，分别算入答案。

这里可以用离散化+普通权值rmq，也可以用动态开点线段树不用离散化

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 233;
int N;
unordered_map<int,int> ump,raw;
ll a[maxn];
ll c1[maxn], c2[maxn];
void add(int x, int v)
{
    for(; x <=