基于python asyncio实现的简单反代
一直想用python实现一个简单的反代工具,最近终于着手做了一下,这篇文章主要是记录一下学习的东西。
参考资料
设计思路
内网穿透
内网穿透的效果就是把只能在内网访问到的设备和服务暴露在公网上。例如内网的网站,俗称内网外入。
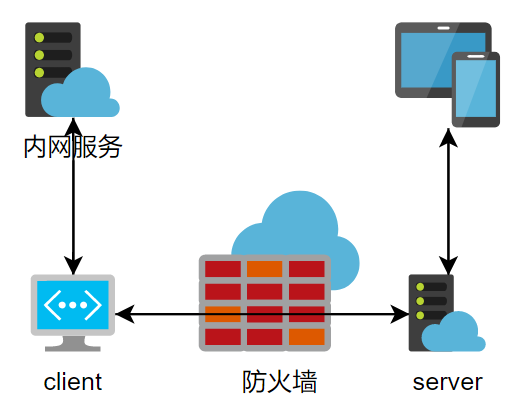
由于个人宽带不一定拥有公网IP,和有对称NAT的存在,所以在内网里可以访问公网的设备能向在公网的服务器请求TCP连接,但服务器却没有办法通过公网向在内网的PC请求连接。
于是可以先由内网设备与在公网的服务器建立一条TCP连接,然后其他设备访问公网服务器的某个端口,所有流量由服务器通过这条连接转发给内网设备。
TCP代理
首先是实现一个基础的TCP代理功能,因为无论是在服务器还是内网设备,都需要转发流量。
原理很简单,就是两个套接字,套接字A用来与服务连接,套接字B用来访问要代理的应用。然后不停地将A收到的发给B,将B收到的发给A。
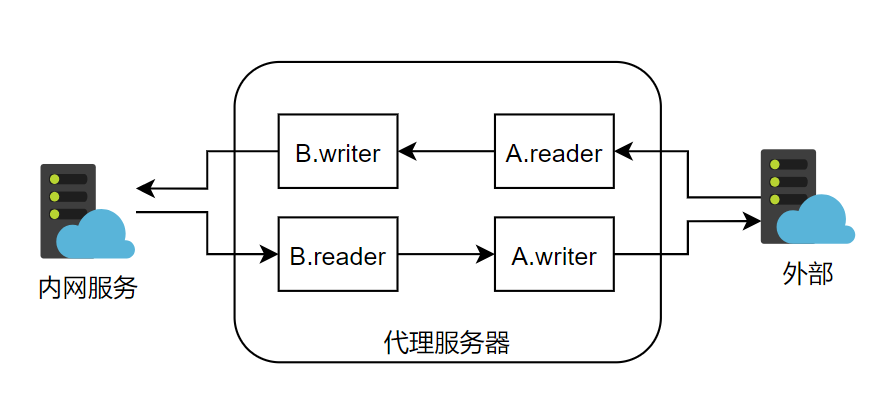
最后我这里用了asyncio的套接字服务asyncio.start_server
监听套接字接收到新的请求以后会回调handle_proxy
async def join_pipe(reader, writer):
try:
while not reader.at_eof():
writer.write(await reader.read(2048))
finally:
writer.close()
async def handle_proxy(local_reader, local_writer):
try:
remote_reader, remote_writer = await asyncio.open_connection(
'jwzx.cqupt.edu.cn', 80
)
task_list = [
asyncio.create_task(join_pipe(remote_reader, local_writer)),
asyncio.create_task(join_pipe(local_reader, remote_writer)),
]
print(f'New TCP connection link { local_writer.get_extra_info("peername") !r} to { remote_writer.get_extra_info("peername") !r}')
done, pending = await asyncio.wait(task_list)
finally:
local_writer.close()
这个转发部分就是我的反代程序的核心部分了。
server与client
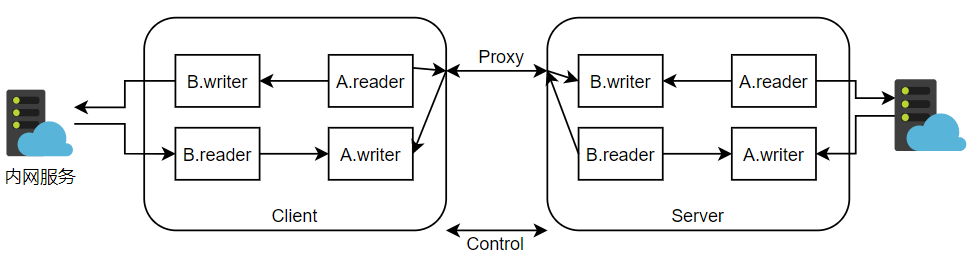
其实Client和Server就是两个几乎一模一样的代理服务器。但又右一点不一样。
考虑到例如http请求,浏览器请求一个页面的时候可能会发多次TCP连接和断开的请求,一旦server和client断开以后,server就没有办法主动连接client了,所以我参考ngrok的设计,也设计了一条Control tunnel的连接一直保持,用来管理用于proxy的通道。
当proxy断开以后,如果接到新的连接请求,就通过Control告诉client,让它与server建立一条新的proxy tunnel,并开始转发。
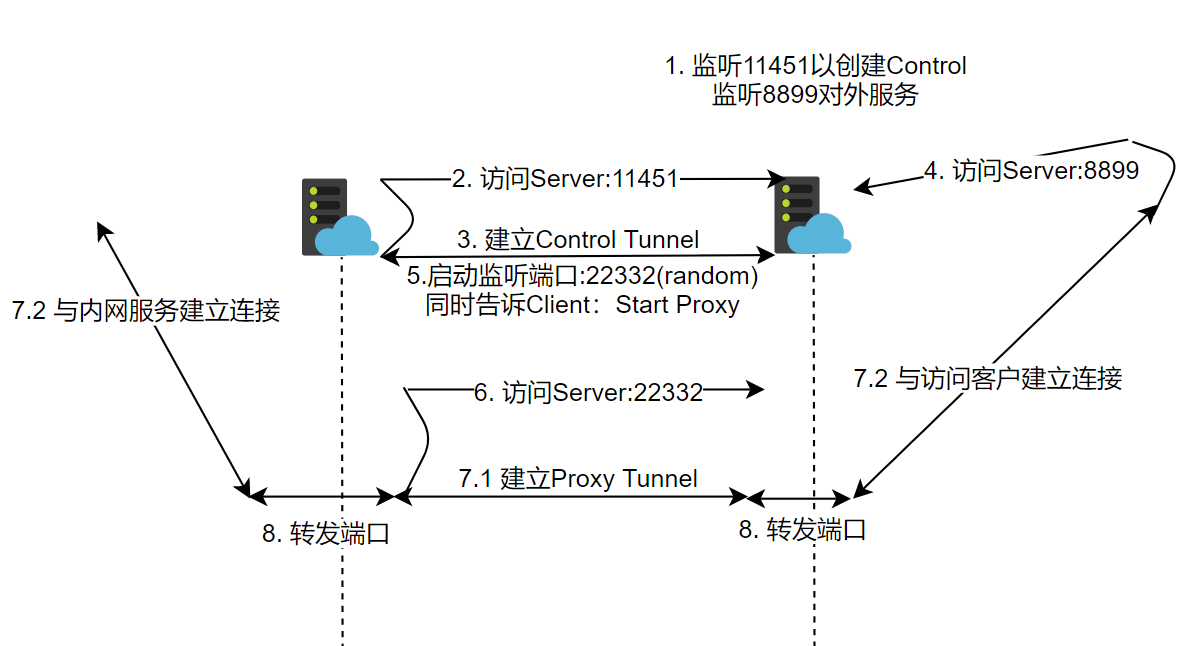
也就是说Server在监听到外部服务的时候会通知Client发一条新的连接Proxy,将Proxy连接的套接字B与外部的套接字A连在一起进行转发。
Client在监听到Control发来的新请求以后会按照信息向新的端口发连接,成功建立Proxy,得到套接字A以后,再开始与内网服务器建立链接,得到套接字B,然后链接这两个套接字开始转发。
然后就按照外部客户的要求,该发送就发送,该断开就断开。这样虽然每次会断开Server与Client的连接,但代码逻辑更简单了,写起来更方便。