【数论】Fibonacci Sum – 20HDU多校1-5
传送门
题意是说给 N, C, K 求这样一个东西:
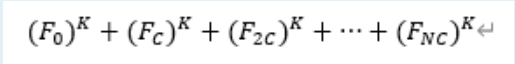
其中F_{NC}表示斐波那契数列的第NC项。
做法是先查一下斐波那契数列的通项公式:
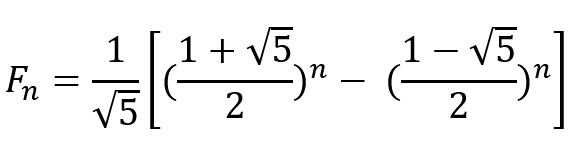
找到其中根号5的二次剩余。
383008016^2 ≡616991993^2≡5 (mod 10^9+9)
然后就可以替换掉通项里的东西。
F_n=C(A^n-B^n)
可得
F_{cn}^k=C^k(A^{cn}-B^{cn})^k
\sum\limits_{i=0}^n F_{ci}^k=C^k\sum\limits_{i=0}^n(A^{ci}-B^{ci})^k
对其二项式展开, 并变换枚举顺序
\sum\limits_{i=0}^nF_{ci}^k= C^k\sum\limits_{i=0}^n \sum\limits_{r=0}^k \binom{k}{r}(A^{ci(k-r)}B^{cir}(-1)^r)
\sum\limits_{i=0}^nF_{ci}^k= C^k \sum\limits_{r=0}^k \binom{k}{r} (-1)^r \sum\limits_{i=0}^n (A^{ci(k-r)}B^{cir})
然后观察到内层的 \sum\limits_{i=0}^n (A^{ci(k-r)}B^{cir}) 其实是以(A^{c(k-r)}B^{cr})为公比的等比数列(几何级数),可以直接使用公式求和。
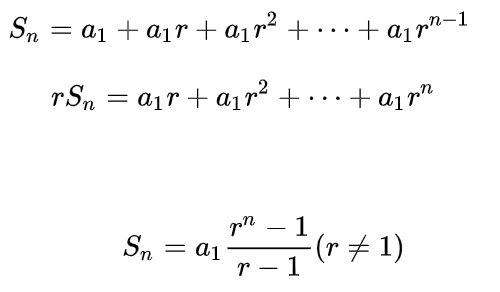
- 注意本题从0累加到n实际上有n + 1项,求几何级数的时候需要注意。但是第0项等于0,所以也可以看作从1开始枚举,用通项的时候单独减去1。两种处理方法都可以。
-
第二个需要注意的点是公式仅适用于r =\not 1。如果r=1直接用r * n或者r*(n+1)即可。取决于上面一步是什么处理方法。
在实际代码中,每一轮的公比实际是上一轮的A和B自乘一个单位,所以可以先预处理。不然这题时间卡的非常紧会T掉。
#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod =